ЭВМ шагает по Москве
Инженер О. НАЛБАНДЯН
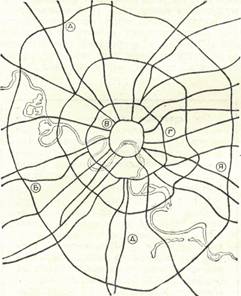 Посмотрите внимательно на изображенный лабиринт. Мысленно попытайтесь из точки А пробраться к точке Я и рассчитайте, сколько времени ушло на поиск правильного пути. Скорее всего несколько секунд. Теперь попытайтесь найти наиболее короткий маршрут. Для этого вам, очевидно, придется сначала найти все пути, измерить длину каждого и выбрать кратчайший. На эту задачу уйдет не менее получаса. Вот, наконец, более сложная задача: проехать от А до Я, заодно побывав в точках Б, В, Г, Д. Можно быть уверенным, что даже самые рьяные любители разгадывать лабиринты откажутся от поисков оптимального пути. Если во много раз увеличить лабиринт, то мы получим столь знакомую нам Москву с ее многочисленными площадями и проспектами, улицами и проездами, тупиками и объездами, светофорами и «кирпичами», многорядным и односторонним движением — короче, столь малознакомую нам Москву с ее транспортной сетью.
Посмотрите внимательно на изображенный лабиринт. Мысленно попытайтесь из точки А пробраться к точке Я и рассчитайте, сколько времени ушло на поиск правильного пути. Скорее всего несколько секунд. Теперь попытайтесь найти наиболее короткий маршрут. Для этого вам, очевидно, придется сначала найти все пути, измерить длину каждого и выбрать кратчайший. На эту задачу уйдет не менее получаса. Вот, наконец, более сложная задача: проехать от А до Я, заодно побывав в точках Б, В, Г, Д. Можно быть уверенным, что даже самые рьяные любители разгадывать лабиринты откажутся от поисков оптимального пути. Если во много раз увеличить лабиринт, то мы получим столь знакомую нам Москву с ее многочисленными площадями и проспектами, улицами и проездами, тупиками и объездами, светофорами и «кирпичами», многорядным и односторонним движением — короче, столь малознакомую нам Москву с ее транспортной сетью.
Как можно было убедиться на приведенном примере, поиски оптимальных транспортных маршрутов сводятся к задачам с огромным числом возможных решений, из которых еще предстоит выбрать наилучшее. Щадя нервы наших читателей, предлагаем самую скромную на первый взгляд из числа подобных задач.
10 заказчиков, живущих в разных точках города, вызвали на дом такси. В 10 других точках находится 10 автомашин. К какому из заказчиков послать каждую из машин? Простой перебор всевозможных вариантов показывает, что число вариантов, подлежащих рассмотрению, равно 3 628 800.
Совершенно очевидно, что даже столь простая задача посильна разве что электронно-вычислительной машине. Тем более что каждый из рассматриваемых вариантов может быть реализован, как мы уже убедились на примере лабиринта, большим числом различных маршрутов. Для того, чтобы выбрать кратчайший маршрут оптимального варианта, ЭВМ должна каждому маршруту приписать его длину, затем сравнить длины маршрутов… Итак, мы сформулировали постановку проблемы: определение с помощью ЭВМ транспортных расстояний между любыми точками Москвы так называемым методом полного перебора.
В самом центре Москвы, неподалеку от стен древнего Кремля, на набережной Мориса Тореза, есть квартал, застроенный старинными домами. В прошлом веке этот район назывался Софийским подворьем. Сюда со всех концов России далеко не оптимальными путями везли купцы свои товары для москвичей. Толстые стены специальной кладки на яичных желтках поддерживали внутри зданий ровную температуру, узкие щелки окон-бойниц надежно защищали от постороннего взора и от непрошеных гостей. Ныне в одном из этих зданий разместился Вычислительный центр Главмосавтотранса — крупнейшего автотранспортного объединения в мире.
С помощью более чем 500 современных вычислительных машин ВЦ контролирует работу более чем 80 автотранспортных предприятий, обслуживающих десятки тысяч заводов, строек, магазинов, школ, вокзалов, аэропортов… Сотрудниками ВЦ, математиками И. Г. Медведовской и Т. М. Великановой, смоделирована и заложена в память машины транспортная карта всей Москвы, позволяющая за ничтожно малое время определить расстояние между любыми точками города.
Нетрудно догадаться, что в реальности приходится рассматривать задачи, во много раз более емкие и сложные, чем предложенная выше. Пунктами назначения могут являться несколько точек города, как, например, при развозке продуктов по магазинам или при выемке писем из почтовых ящиков. Если в уже рассмотренной задаче предположить, что каждая из десяти машин должна побывать в трех разных точках, то количество вариантов, подлежащих рассмотрению, будет выражаться числом с тридцатью одним нулем.
Pages: 1 2
